Куликов В.

"Estrella" - чертеж Великой Пирамиды в горах Наска.

Итак, в чертеже, одним из основных правил является правило последовательного деления целого на 2. В прямоугольной системе мы делим ячейки на квадраты, в полярной системе - полную окружность. Квадрат 8х8 и 16 лучей представляют собой 3-ю стадию этого процесса (2^3). Обнаруживаются признаки предыдущих стадий (деление на 2 и на 4), что говорит о внутренней динамике и возможности продолжения этого процесса, т.е деление на 16, 32, 64, и т.д.

Рассмотрим еще одну особенность срединной части чертежа:

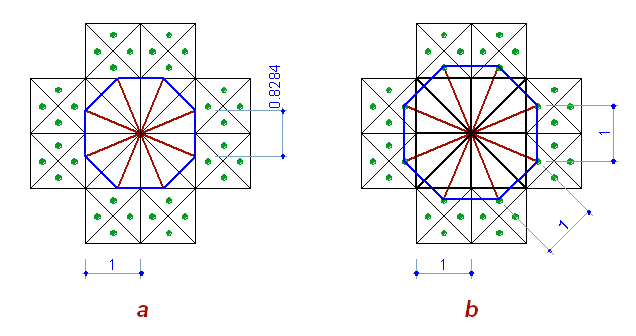
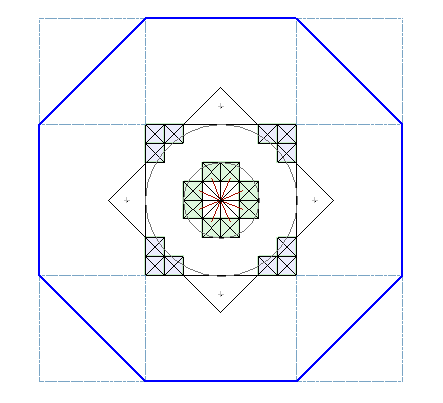
Рис. 1

Лучи 3-й стадии образуют правильный восьмиугольник при пересечении со сторонами ячеек (Рис. 1.a). (казалось бы - красиво, что еще нужно?)

Но на геоглифе эти лучи продлены до маркировочных точек (Рис. 1.b). Образуемый таким образом восьмиугольник имеет сторону равную стороне ячейки!

Периметр этого восьмиугольника равен 8 или:

а) периметру квадрата 2х2, который окружают замаркированные ячейки

б) стороне основного квадрата (8 ячеек).

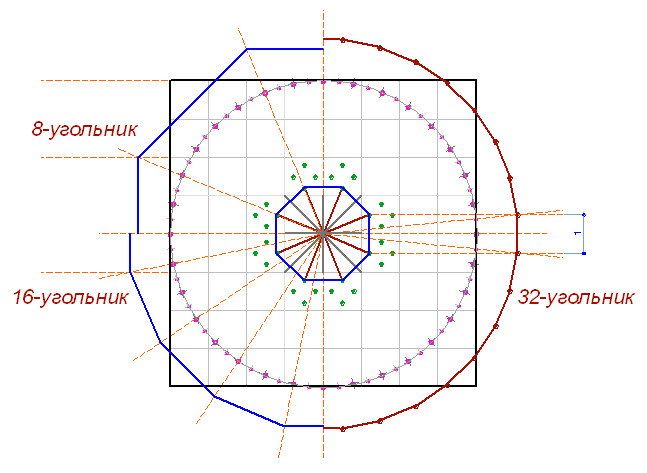
Но полярная система, как мы уже говорили, стремится к окружности. Значит, последовательно увеличивая количество сторон в 2 раза, многоугольник будет приближаться к окружности. А сохраняя связь с ортогональной системой (сторона кратна модулю), мы будем получать окружность с периметром модульного квадрата!

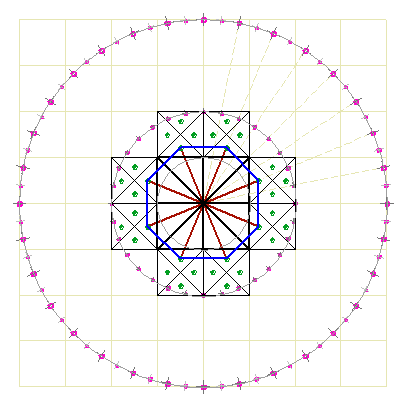
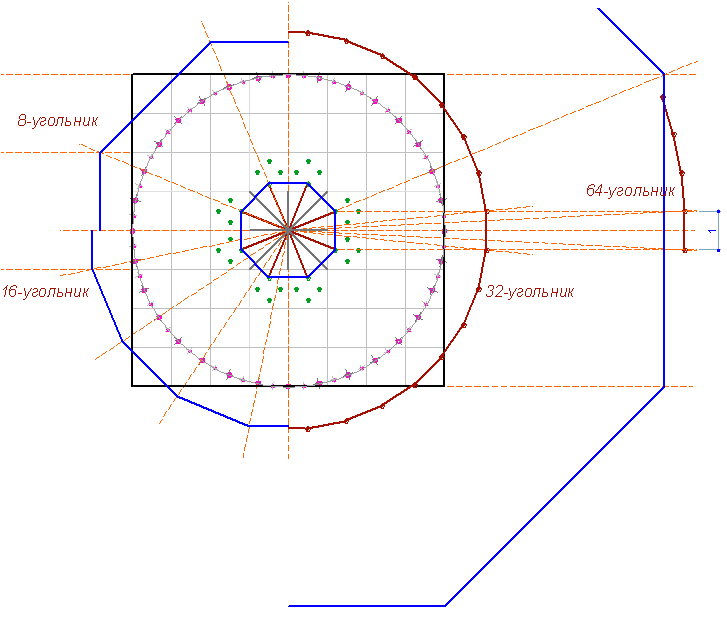
В поддержку такого вывода на геоглифе обнаруживается окружность с делением на 32 части (R=2), а самая большая окружность (R=4) делится на 64 части:

Итак, "звезда" демонстрирует отношения окружности и квадрата, и механизм последовательного приближения к точке, где периметр окружности будет равен периметру квадрата. А так, как деление на двое можно продолжать до бесконечности, то точка эта практически недостижима. Эта взаимосвязь в современной математике выражается через отношение диаметра окружности к ее длине числом "пи".

Для истории квадратуры круга такое решение является фантастическим, если учесть попытки датировать геоглифы промежутком от 500 до н.э. до 500 н.э. Хотя датирование это относится к племенам наска, населявшим в то время эту территорию, и, как я думаю, к созданию геоглифов отношение не имеющие.

В древности отношение периметров (или площадей) окружности и квадрата (число пи) пытались выразить в виде целочисленного отношения (рационального числа). Т.е. число пи пытались представить в виде дроби (256/81, 4* (11/14)). Архимед, посредством построения правильных многоугольников с числом сторон 6, 12, 24, 48 и 96 сделал вывод что  3 10/71 < пи < 3 1/7. Практически это первая попытка построений с последовательным приближением, попытка создания алгоритма приближенного вычисления. Но с помощью него он пытался найти отношение целых чисел равное пи.

И только Г. Лейбниц в 17 в. доказал что пи - величина иррациональная, что представить ее в виде конечной  дроби не возможно.

Полярная система формирует правильный многоугольник со стороной, соответствующей размеру модульной ячейки на этой же стадии деления системы на 2.

Значит при последовательном развитии всей композиции мы должны получать многоугольники со стороной равной ячейке модульной системы, увеличивая число сторон как степень 2. И периметр его будет равен периметру квадрата.

Остается научиться пользоваться матрицей многоугольника (назовем ее так).

Для этого проследим развитие многоугольника на стадиях развития системы.

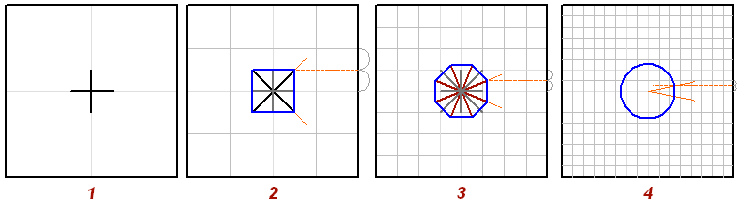
Рис. 3

Вершина многоугольника на стадии определяется пересечением нового луча с линией, проходящей через середину модульной ячейки (Рис. 3.2).

Периметры всех этих многоугольников равны стороне основного квадрата.

Аналогично полярной матрице (Глава 1. Рис. 9), матрица многоугольника, увеличенная до масштаба всей композиции, сгенерирует серию многоугольников с периметром раным периметру основного квадрата:

Рис. 4

На этом этапе задействованы 32 разметочные точки на большой окружности, а их там 64. К тому же сторона 8-угольника на Рис. 4 равна только половине основного квадрата. Т.е. предполагается еще развитие этой схемы до 64-х угольника, сторона которого будет равна ячейке нашей композиции, а периметр будет равен периметру квадрата 16х16:

Рис. 5

Получаем инструкцию по эксплуатации "матрицы многоугольников":

Для получения серии многоугольников, стремящихся к окружности заданного квадрата, нужно смасштабировать матрицу до размеров квадрата и "запустить" механизм последовательного деления систем на двое.:)

Многоугольники построенные на основании квадрата 16х16 - являются продолжением развития композиции в случае сохранения размера ячейки. Т.е. ячейка остается той же, а увеличивается вся система. (обратный прцесс делению на двое).

Таким образом матрица многоугольника может генерировать окружность, с периметром заданного квадрата.

Сторона восьмиугольника, построенного с помощью матрицы на квадрате 16х16, будет равна 8, т.е. стороне основного квадрата композиции. А расстояние от центра до вершин получаемых многоугольников, будет стремиться к радиусу описанной окружности, 1/8 часть периметра которой, будет также приближаться к этой длине.

К тому же этот восьмиугольник является полярной матрицей для нашей звезды:

Рис. 6

Итак, 16 лучей с разметочными точками на геоглифе, демонстрируют следующее правило:

При последовательном делении квадрата и окружности пополам, пересечение линий деления квадрата с осями делящими окружность, образуются точки, являющиеся вершинами многоугольника, стороны которого кратны стороне квадрата, а периметр его равен периметру квадрата.

Звезда не только демонстрирует противоречия, но и показывает связь квадрата и круга. И не просто связь, а точки где две различные системы пересекаются и работают совместно. Восьмиугольник, являющийся результатом пересечения двух квадратов, является связующим звеном между квадратом и окружностью, кубом и сферой. Двух совершенно противоположных систем - ортогональной (2-х или 3х мерной) пространственной системы и полярной или радиальной системы.

Задан механизм приближенного вычисления радиуса окружности с периметром, равным периметру заданного квадрата. Не в виде какого либо-конкретного отношения (например 355 по горизонтали и 113 по вертикали), а в виде алгоритма, с помощью которого можно достигнуть любой требуемой точности, повторяя процесс деления на 2 и построения следующего многоугольника.

Логика рекурсивной композиции определяет направления развития как во внутрь, так и во вне. Звезда является упакованным в геометрию изящным изложением законов и правил, по которым работает система.

<<< Глава 3 >>>

Вводная часть.

Глава 1. Информативные и семантические признаки композиции.

Глава 2. Вложенность или рекурсивность системы.

Глава 3. Многоугольники и квадратура круга.

Глава 4. Окружности и их периметры.

Глава 5. Пирамиды.

Приложение. Точность чертежа.