|
 |
 |
||||
 |
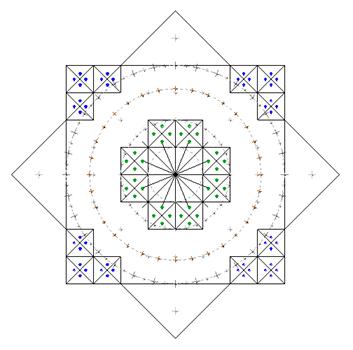
"Estrella" - чертеж Великой Пирамиды в горах Наска.
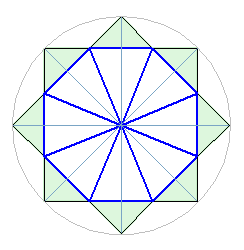
Рис. 1 С добавлением окружностей, система приобретает новый толчок к деформациям. На фоне окружности слабая способность ортогональной системы к симметрии, вынуждает ее модифицировать внутреннюю структуру элементов, добавляя новые правила в их взаимоотношения.
Попробуем посмотреть на другой слой нашей композиции.
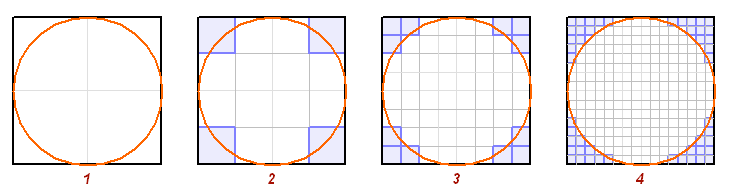
С сохранением модульной структуры, квадрат может достигать близости с окружностью: с уменьшением размера ячейки усиливается его способность создать множество равноудаленных элементов от центра.
Иными словами обычная дискретизация (квантование по уровню)).: Поэтапно делим ячейки квадрата пополам, и отсекаем не принадлежащие кругу ячейки.
Рис. 3 Обратим внимание на стадию 2 и 3 этого повторяемого процесса деления модульной клетки. Стадия 2 – это наша матрица Qa-Qb (Рис. 14.b. Гл. 1.), позаимствованная из правильного восьмиугольника. И квадраты Qb оказываются внешними по отношению к окружности. Стадия 3 – это развитие нашего процесса отсечения лишних квадратов при модульной клетке равной 1/8 стороны квадрата, но это и основной квадрат звезды геоглифа как и на Рис. 1.
Для поддержания равновесия и порядка добавим отсутствующие квадраты Qa, и посмотрим как они будут себя вести в процессе:
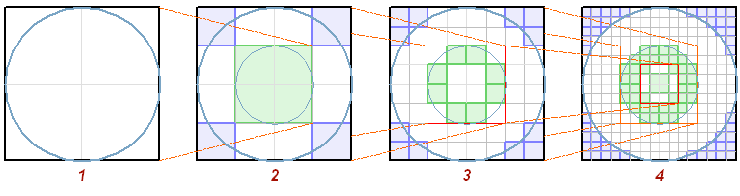
Рис. 4 Стадия 3 (8х8) – просто великолепна. Она содержит в себе все предыдущие (4х4 - стадия 2 и пустой квадрат 2х2 – стадия 1), и показывает нам механизм в действии. Процесс можно продолжать до бесконечности. В результате квадрат будет "подгонять" свои ячейки к окружности и с каждой итерацией это соответствие будет точнее. Это свойство фрактальных систем. Замаркированные ячейки демонстрируют важное свойство системы - структурную рекурсивность. (Когда на всех уровнях используется самоподобная структура). Кроме того, поэтапно, наблюдается чередование негативных (обратных) изменений: пустота заменяется маркировкой на следующей стадии.
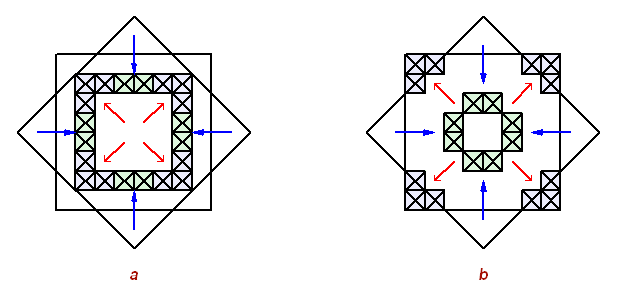
Рис. 5 Раскрывается "смысл зонирования" замаркированных ячеек: Qb – это отсекаемые "центробежными" усилиями кванты пространства квадрата и "центростремительные" элементы Qa, удовлетворяющие условию равноудаленности от центра. Или Qb – зона расширения, Qa – зона сжатия.
Тот факт, что композиция состоит из элементов, идентичных по структуре общей композиции, позволяет говорить о рекурсивных ее свойствах. А так как вложенные композиции представляют саму систему, но на предыдущей стадии развития, говорит о внутренней динамике фрактального процесса, результатом которого является достижение некоторой цели, находящейся за пределами бесконечности.
Например: Количество ячеек внутри окружности будет стремиться к площади круга, а количество примыкающих к окружности ячеек, будет стремиться к длине окружности. Эти величины связаны с линейным размером радиуса окружности посредством иррационального числа пи, и следовательно точный результат недостижим в принципе. И направленный в бесконечность процесс деления модульной сетки с каждой итерацией будет приближать к истинной окружности.
Мне кажется это очень важный слой чертежа. Если предположить, что он тоже является иллюстративным (из преемственности родительского процесса), то можно сделать вывод: Речь в чертеже будет идти о повторяемых процессах уточнения или дискретизации, с целью приблизиться к бесконечно удаленному идеальному решению. А это значит, из общности законов внутри системы, что и другие элементы должны рассматриваться в динамике повторяемых процессов. Композиция содержит элементы, находящиеся в явной взаимосвязи между собой. Лучи, маркировочные точки, отмеченные ячейки демонстрируют одну и ту же контекстную композиционную тему. Совпадения? Накладываясь на единую логическую основу, они не могут быть просто совпадениями. Явно определенная знаковая функция вспомогательных элементов, говорит о том, что кто-то хотел именно привлечь внимание к прочтению геометрии геоглифа. Говорить о том, что это просто эстетические изыскания в области геометрической орнаменталистики, подобно украшению глиняного сосудика, очень и очень сложно. Очень как-то не по себе писать о дискретизации, о фрактальном приближении, разглядывая группу геометрических примитивов времен практически первобытных. Кто мог так легко манипулировать многоуровневыми понятиями, расставляя крестики в клеточках, размерами в десятки метров на расстояниях в несколько сот метров? Для кого этот "кто-то" пытался что-то иллюстрировать и с таким вниманием относится к его пониманию?.. Случайны ли эти совпадения? Я старался следовать тому, что я вижу. Это как обнаружение фигурки какой-нибудь медведицы среди множества звезд. Только геоглиф предоставляет множество закономерностей, и какие-то из них ярче и сгруппированы в определенные линии, из которых получается объемная модель разгуливающей в анимации медведицы. Можно относиться к ней как к приятной галлюцинации, только мне кажется, лучше подобрать под себя ноги и иные выступающие части тела, чтобы она, ненароком, не наступила. Глава 1. Информативные и семантические признаки композиции. Глава 2. Вложенность или рекурсивность системы. Глава 3. Многоугольники и квадратура круга. |
 |
||||
 |
 |
 |