Куликов В.

"Estrella" - чертеж Великой Пирамиды в горах Наска.

Прежде всего, нужно заметить, что мы имеем восьмиконечную звезду, отличающуюся от "правильной" восьмиконечной звезды, тем что состоит она из разных по размеру квадратов, и это объясняется тем, что наша композиция строится по модульной прямоугольной сетке. Восьмиугольник, образуемый пересечением квадратов получается не равносторонний (Рис. 2.а).

Рис. 2

В правильной звезде (Рис. 2.b), построенной разворотом двух равновеликих квадратов, все уравновешено: отсекаемые треугольники равны между собой, в результате остается совершенно правильный восьмиугольник, имеет 16 осей симметрии повернутые на одинаковый угол относительно друг друга (360/16). Эти свойства приближают правильную звезду к окружности.

Иными словами, она обладает свойствами полярной или радиальной системы, где равновеликие величины равноудалены от центра.

С остальными - проблема. Возможны два варианта:

a) подчиниться правилу ортогональной системы и разделить пополам сторону ячейки (вариант а, Рис. 5);

b) либо по правилу правильной звезды разделить пополам угол (вариант b, Рис. 5):

Рис. 5

В первом случае мы следуем правилу общей композиции, но сталкиваемся с ее недостатком: угол AOB не равен углу BOC.

Во втором случае, мы получаем 16 лучей равномерно распределенных по окружности, но теряем равномерное деление сторон квадрата.

(то же, но увеличим центральную часть)

Рис. 6

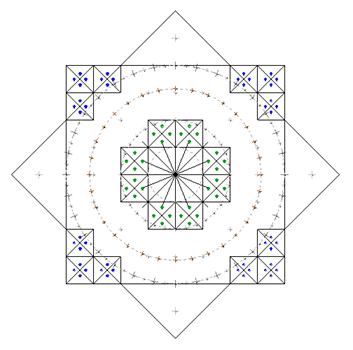
При неточности скального рисунка (а там погрешности в этом масштабе около 1-2 толщины линии), было бы трудно отличить какой именно вариант там используется. Лучевая звезда в разных вариантах выглядела бы почти одинаково.

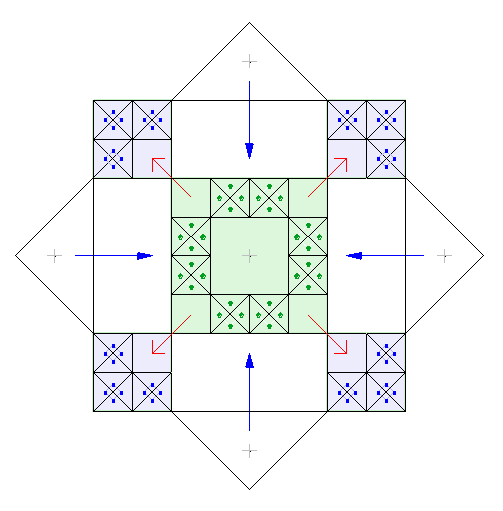
Но об этом позаботились. На геоглифе точки через которые проходит луч обозначили:

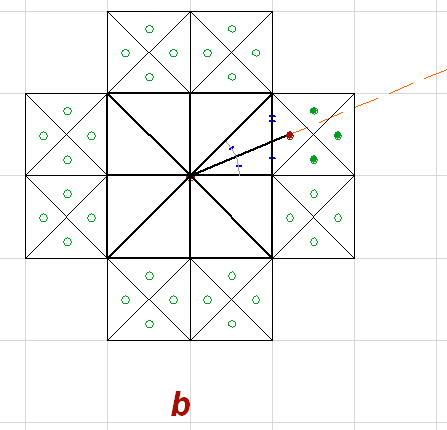
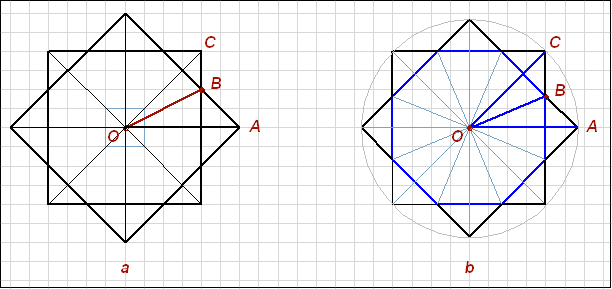
Рис. 7

Точка лежит на середине высоты ячейки, но сдвинута от вертикальной стороны.

Только в этой точке биссектриса угла пересечет горизонтальную ось ячейки.

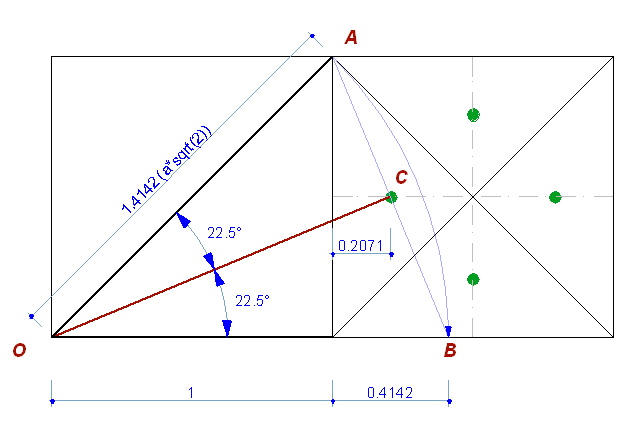
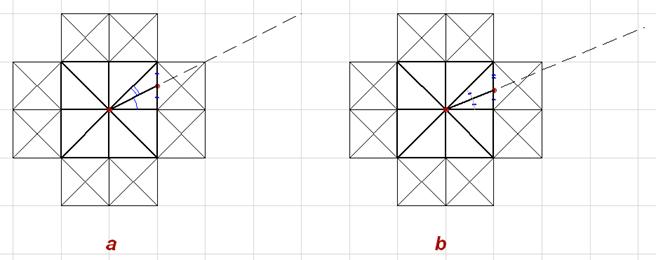
Рис. 8

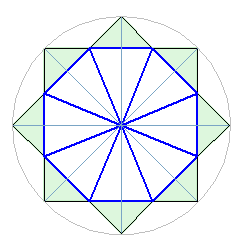
Именно деление угла на равные части используется при построении 16 лучей. Образуется угол правильного восьмиугольника, а в основе звезды лежит не правильный, "ортогональный" восьмиугольник. Это противоречит логике ортогонального модульного построения общей композиции, но проецирует ту же логику (деление на 2) на радиальную систему. Таким образом, в композицию добавляется полярная система.

Обнаруживается конфликт (в противопоставлении) двух различных геометрических систем : правильной восьмиугольной звезды, построенной по принципам полярной системы, и "неправильной", построенной на ортогональной модульной основе.

Этот конфликт заставляет систему модифицировать структуру внутренних связей, в стремлении к равновесию.

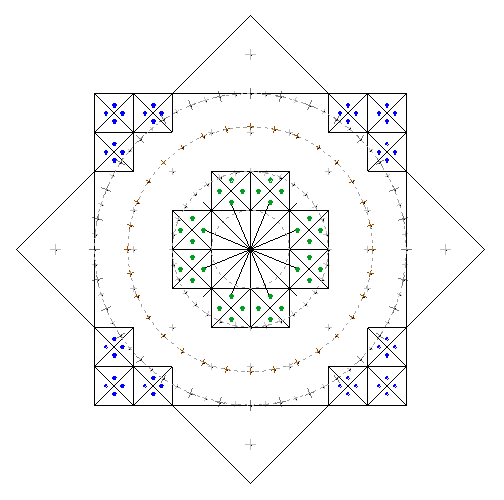
А вот для чего тогда остальные три точки?

Формируя собой диагонально повернутый квадрат, они показывают, что точки лежат именно на серединных осях ячейки, а не где-то ближе или дальше к вершине. И диагональные перекрестия ячеек, тоже помогают воспринять неточный рисунок правильно.

То есть, маркировка в (этом случае) нанесена для того, чтобы указать на то, что именно угол делится пополам лучами, а не сторона ячейки, как можно было бы, следуя логике общей композиции, предположить.

В противном случае, построив биссектрисы достаточно было бы остановить луч на стороне квадрата, в крайнем случае, довести до первой точки. Но нам даются именно все четыре точки, которые ассоциативно связывается в квадрат и с его помощью хорошо прочитываются правила построения.

Маркировочные точки, получается, нанесены не случайно, и не из эстетических соображений, а как уточнение чертежа, дающее гарантию прочесть чертеж правильно.

Почти одинаковая величина углов, получаемых в разных вариантах, может внести ошибку при прочтении, и, с расчетом того, что изменение логики построения может оказаться не замеченным, на этом моменте акцентируется внимание. Точки активно показывают, подчеркивают, что именно правила "правильной восьмиконечной звезды" работают в этой части чертежа. А это говорит о том, что чертеж обладает свойствами иллюстрации, т.е. он нарисован с учетом того что его будут читать. Маркировка, как семантические элементы, используется в качестве пояснений к чертежу, но для кого предназначены эти пояснения? И почему так важно одинаковые там углы или нет? Единственной ли является "проблема построения лучей", или чертеж содержит гораздо больше информации?

Выводы об иллюстративном, указательном характере маркировки подтверждаются и следующим.

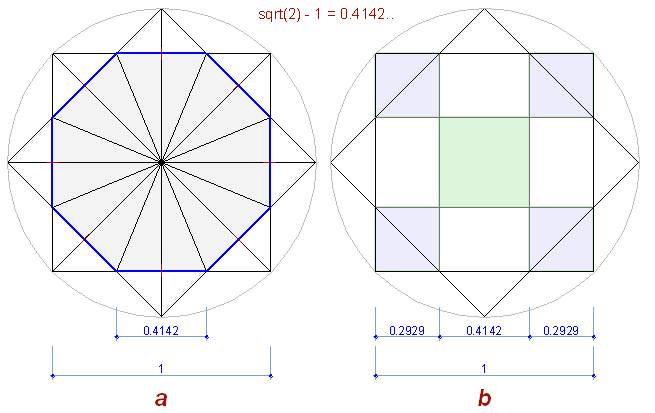
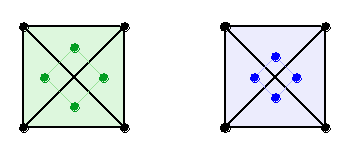
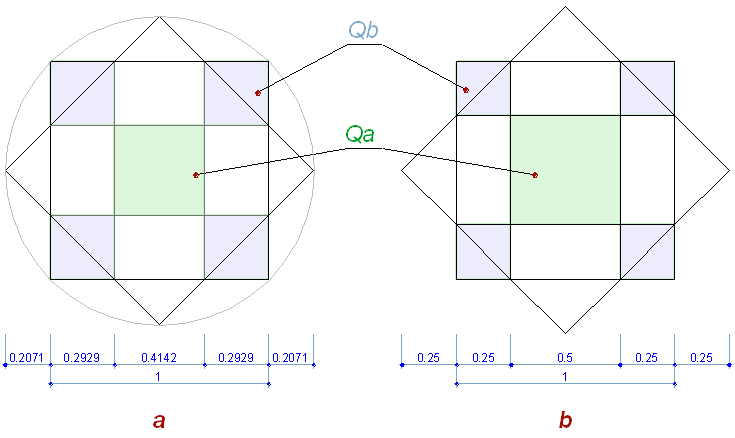
Рис. 9

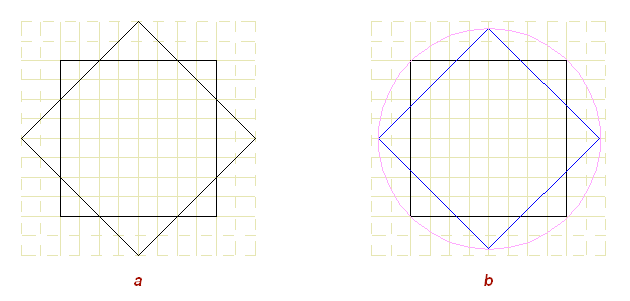
При пересечении, два повернутых квадрата образуют правильный восьмиугольник (Рис. 9.a), со стороной равной sqrt(2) – 1 (при стороне квадрата = 1). Правильный восьмиугольник основан на пропорциональных отношениях стороны квадрата к его гипотенузе, выражающееся через корень квадратный из 2. И деление квадрата (Рис. 9.b) вершинами восьмиугольника происходит тоже с таким же пропорциональным коэффициентом, на иррациональные части.

Повернув этот рисунок (Рис. 9.b) на 45°, увидим, что это и есть маркировочные квадраты, обозначенные точками на геоглифе:

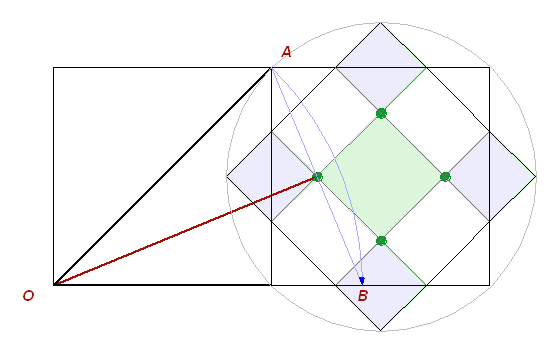
Рис. 10

Точки геоглифа в ячейках соответствуют иррациональным ячейкам квадрата правильного восьмиугольника.

Остается догадаться - где используются меньшие (синие) квадраты?.

20 из 64-х ячеек основного квадрата "замаркированы".

Рис. 11

На снимках геоглифа хорошо заметно, что размеры маркировочных квадратов различаются. Ячейки основного квадрата, расположенные в углах (12 шт.), маркируются явно меньшими по размеру квадратиками (я обозначил их синими точками), чем ячейки расположенные вблизи центра (8 шт. – зеленые точки). (Основной квадрат 8х8, а диагональ повернутого квадрата – 12)

Назовем их для удобства Qа – больший, и Qb – меньший:

Рис. 12

Таким образом ячейки делятся на четыре типа: сначала на пустые и замаркированные, затем замаркированные большим квадратом Qа и малым Qb.

Если мы наложим пропорциональную матрицу, полученную на Рис. 9.b то заметим, что схема маркировки ячеек Qа и Qb квадратами совпадает с расположением соответствующих квадратов матрицы:

Рис. 13

В неправильной звезде пропорции матрицы адаптируются к модульным отношениям:

Рис. 14

И так мы видим, что матрица Qa-Qb квадратов (Рис. 14), включена в композицию как система пропорциональных отношений правильного восьмиугольника для построения 16-ти лучей, и выступает еще в качестве схемы маркировки ячеек, связывая прямоугольную и полярную систему. Расположение замаркированных ячеек еще раз подводит нас к тому, речь идет об отношениях полярной и ортогональной системы.

Что получается? Из центра звезды берет начало геометрия радиальной системы, а в результате нарисована прямоугольная звезда, подчиненная правилам ортогональной модульности.

Нарисовать уточек в углах, а по середине лодочку – это еще можно понять. Но рисовать квадратик со стороной относящейся к стороне ячейки в пропорциях построения радиальной системы и наслаждаться радостью того, как он выглядит, распределяя его по кругу в прямоугольной системе в виде замысловатых точек – это уже сложнее отнести к развлечению.

Получается, что расположение помеченных ячеек, размеры маркировочных квадратов являются явно демонстрируемыми признаками включения в общую композицию, построенную на модульной ортогональной основе, элементов радиальной системы правильной восьмиконечной звезды. Намекают на близость этих систем и на отличия, которые в корне меняют внутренние свойства композиции. Наличие таких внутренних связей между элементами, убеждает меня в том, что геоглиф носит информативный характер.

Технология элементов-подсказок, включенных в общую схему и так гармонично в ней работающих, исполняя функцию указательных знаков - не очень типична для традиционных методов изложения информации, берущих свое начало от математиков-философов древнего мира. Эстетическая составляющая является лишь канвой, основой для изложения информации, подобно игре слов в поэтическом изложении, несущей послойно уложенный глубинный смысл, явно не проявляющийся в конкретных словах. Л. Кэролу возможно доставляло удовольствие упаковывать математические измышления в забавные стихотворения для маленькой девочки. Но он имел образование соответствующее.

Каждый включаемый элемент в композицию, является значимым носителем некоторой информации, своего рода символом некоторого геометрического языка.

И мы рассмотрели только иллюстративный, демонстрационный характер композиции.

<<< Глава 1 >>>

Вводная часть.

Глава 1. Информативные и семантические признаки композиции.

Глава 2. Вложенность или рекурсивность системы.

Глава 3. Многоугольники и квадратура круга.

Глава 4. Окружности и их периметры.

Глава 5. Пирамиды.

Приложение. Точность чертежа.