|
 |
 |
 |
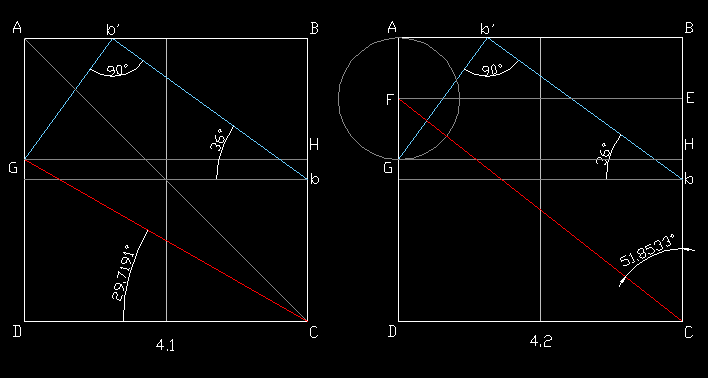
Александр Темаров "Гизехский капкан" Приложение Вычисление периметра и площади круга с циркулем и линейкой (приближенный метод). Из середины стороны BC квадрата ABCD, AB=2R, проведем линию под углом 36° до пересечения со стороной AB в точке b'. Из этой точки проведем перпендикуляр к bb' до пересечения со стороной AD в точке G (рис.4.1). Периметр прямоугольника ABGH примерно равен периметру круга с радиусом R=AB.
Теоретическое значение угла GCD может быть получено из выражения: p=2pR=2a+2x=2(2R+Rtgf)=4R(1+tgf); tgf=p/2-1; f=29.7176°; таким образом, погрешность метода составляет 1- 2p /(4(1+tg29.7191°))=0.000023, т.е. 0.0023%. На рис.4.2 показано, как модифицировать предыдущее построение, чтобы приблизительно вычислить площадь круга с погрешностью не более 0.0023%. Для этого достаточно разделить отрезок AG пополам (точка F). Площадь прямоугольника CDEF примерно равна площади круга с радиусом R=CD/2. |
 |
 |
 |
 |