 |
Другие работы автора
Александр Темаров "Гизехский
капкан"
1. Плато Гиза.
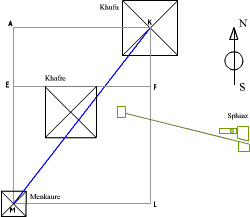
Топографический план.
|
1. Пирамида Хеопса - сверху;
2. Пирамида Хефрена -
посередине;
3. Пирамида Микерина - внизу.
Даже "сырые" исходные
данные позволяют сделать
предварительный вывод о
наличии закономерности в
расположении пирамид на плато,
если за основу геометрического
построения взять
прямоугольник, в углах
которого находятся 1я и 3я
пирамиды. Стороны
прямоугольника параллельны
сторонам света (отклонение оси
1й пирамиды от направления
север-юг составляет 0.0041°).
Cеверная сторона 2й пирамиды
делит прямоугольник в
соотношении 1:2 (высота желтой
части вдвое больше высоты
зеленой при равной ширине).
Ошибка пренебрежимо мала и
составляет от 4 до 12 см для
западного и восточного углов 2й
пирамиды.
|
|
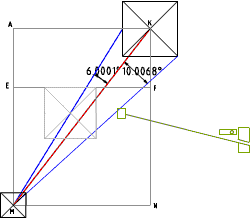
Угловое расстояние между
серединой западной стороны 1й
пирамиды и ее юго-восточным
углом составляет 16.0069° , если
смотреть из центра 3й пирамиды.
Линия KM, соединяющая вершины 1й
и 3й пирамид, делит этот угол в
на две части: 6.0001° и 10.0068°. |
|
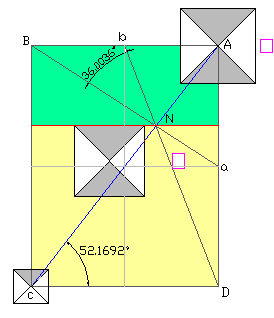 |
Угол между "полудиагоналями",
соединяющего середины сторон с
противолежащими углами
прямоугольника составляет
почти точно 36° (36.0036°).
Это
совпадение имеет неожиданное
продолжение: оказывается,
используя угол в 36°, можно с
помощью простых
геометрических построений
вычислить площадь и периметр
круга с точностью с
погрешностью в 0.171% и даже
меньшей - до 0.0023%!
Угол в основании ACD
составляет величину 52.17°,
которая не "вписывается" в
классические геометрические
конструкции (золотое сечение,
квадратура круга, треугольник 3-4-5
и др.). Тем не менее, наличие "скрытого"
угла в 36° дает основания
использовать 36° для дальнейших
построенией. Кроме того, угол в
36° связан с золотым сечением
очень простым способом:
|
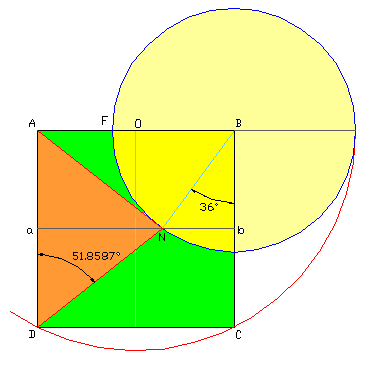 |
Возьмем
квадрат ABCD; проведем
окружность с центром в точке О
- середине AB, радиусом R=OC=OD.
Известно, что при таком
построении длина отрезка BF=j*AB; где j=0.618 - знаменитое
золотое сечение, для которого
справедливо выражение j +1 = 1/j .
Построим
окружность радиусом BF с
центром в точке B. Точка
пересечения окружности с
серединной линией ab
квадрата ABCD дает искомый угол bBN,
равный 36°.
Далее, измерив углол ADN,
получим величину 51.8587°. Этот
угол близок к наклону 1й
пирамиды 51.85°, и, конечно же, к
знакомой величине arctan(4/p) =51.8538° - углу
наклона треугольника, площадь
которого равна площади круга с
диаметром, равным высоте
треугольника.
Но у данного построения есть
еще одна особенность. Чтобы
увидеть ее, вернемся к
топографическому плану плато
Гиза.
|
Дальше
|
 |















